Q値更新
Q学習のメイン、Q値を管理しているプログラムをみていく。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
import numpy as np import Const import re """Q値クラス """ class Qtable: def __init__(self): self.table = {} #Q値テーブル def update(self,key,act): #デバック用 Q値テーブルを1行作成 if key in self.table: self.table[key] = act else: self.table[key] = act def get(self,key): #状態情報から全Q値を取得 if key not in self.table.keys(): #Q値がなかったら新規作成 act = np.zeros((Const.BANSU,Const.BANSU)) """状態により不要なQ値(状態により既に手が打たれているマス目がある、このQ値(行動)は打てないので不要) が影響を及ぼさないように最小値を設定 ○×○ × × -> 状態:212101012 -> 2,1に該当するQ値不要->最小値設定 ×○ """ work = str(Const.BATU)+'|'+str(Const.MARU) m = re.search(work, key) a = [m.start() for m in re.finditer(work, key)] #状態情報から既に打たれている箇所を検索 for idx in a: q, mod = divmod(idx, Const.BANSU) act[q][mod] = Const.MIN_VALUE self.table[key] = act return self.table[key] def disp(self): #状態:Q値全表示 for key, values in self.table.items(): moji = "" for value in values: moji += str(value) print("key:" + key + "values:" + moji) def getMaxTable(self,key): #状態の最大Q値を取得 data = self.get(key) return np.nanmax(data) def cal(self,key1,key2,x,y,win): #Q値更新 data = self.get(key1) #Q値取得 if key2 != 0: #次の手有り data[x][y] = data[x][y] + Const.GAKUSYU*(win+Const.WARIBIKI*(self.getMaxTable(key2))-data[x][y]) else: #勝敗がついた場合は次の手のQ値最大値は不要 data[x][y] = data[x][y] + Const.GAKUSYU*(win-data[x][y]) self.table[key1] = data |
テーブル構造
Q値を管理するテーブルはPythonのdict(辞書)機能により実現している。この辞書機能はいわゆる連想配列であり、キーワードにより値を照会、設定できる。プログラムでは9行目で定義している。
|
9 |
self.table = {} #Q値テーブル |
キーワードは前回(AI Q学習#2)紹介した、棋盤情報を文字列化したモノを利用する。これにより棋盤の全パターンの情報を辞書として登録できる。
このキーワードから取得されるデーターが行動毎のQ値である。三目の並べの行動は「マス目に手を打つ」ことから、行動数は最大9(3×3)となる。
データを3×3の二次元配列にしたが、9の一次元配列にした方がハンドリングしやすかったと反省している。
キー作成、データ初期化は関数get()で行っている。|
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
def get(self,key): #状態情報から全Q値を取得 if key not in self.table.keys(): #Q値がなかったら新規作成 act = np.zeros((Const.BANSU,Const.BANSU)) """状態により不要なQ値(状態により既に手が打たれているマス目がある、このQ値(行動)は打てないので不要) が影響を及ぼさないように最小値を設定 ○×○ × × -> 状態:212101012 -> 2,1に該当するQ値不要->最小値設定 ×○ """ work = str(Const.BATU)+'|'+str(Const.MARU) m = re.search(work, key) a = [m.start() for m in re.finditer(work, key)] #状態情報から既に打たれている箇所を検索 for idx in a: q, mod = divmod(idx, Const.BANSU) act[q][mod] = Const.MIN_VALUE self.table[key] = act return self.table[key] |
引数のキーワードからデータ(Q値)を返す関数だが、キーワードが登録されてないならキーワードを作成しデータを初期化する。
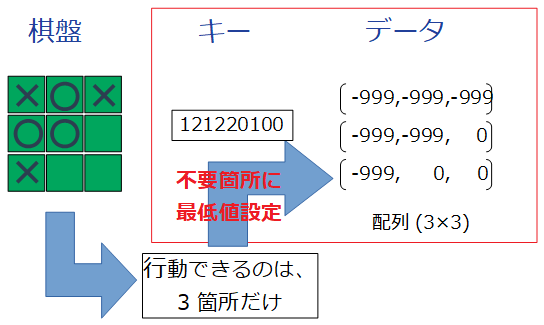
ここで問題が発生した。上記の状態だと既に6箇所に手が打たれている。そのため次の行動は3箇所と限られているので、6箇所分のQ値は不要だ。当初はそのまま0を設定していたが、デバックを行うにつれこの0が悪さをしていることに気付いた。そこで不要なQ値へ最低値を設定するようにした。
Q値更新
Q値の更新を行っているのが関数cal()である。
|
44 45 46 47 48 49 50 51 52 53 54 55 |
def getMaxTable(self,key): #状態の最大Q値を取得 data = self.get(key) return np.nanmax(data) def cal(self,key1,key2,x,y,win): #Q値更新 data = self.get(key1) #Q値取得 if key2 != 0: #次の手有り data[x][y] = data[x][y] + Const.GAKUSYU*(win+Const.WARIBIKI*(self.getMaxTable(key2))-data[x][y]) else: #勝敗がついた場合は次の手のQ値最大値は不要 data[x][y] = data[x][y] + Const.GAKUSYU*(win-data[x][y]) self.table[key1] = data |
この計算は以前(AI Q学習)紹介した数式をプログラム化している。数式と若干違うところは、「次の手のQ値最大値取得」だ。デバックを進めていくと「次の手のQ値最大値取得」ができない、取得しても無駄な場合があることがわかった。
まずAIが勝利した場合は次の行動は無いので値は取得できない。次に相手が勝利した場合は「次の手のQ値最大値」は必ず0になるので無駄とわかった。そこで、50行目のif文で「次の手のQ値最大値取得」を行うかの分岐を行っている。